PHYSICAL MODEL:
An Erbium Doped Fiber Amplifier (EDFA) consists of a piece of fiber of length L, whose core is uniformly doped with Erbium ions. Such ions can be thought of as simple two-level systems, i.e., they can have only two energy states: 1) a fundamental state and 2) an excited state.
A strong ``pump'' laser light at the proper wavelength (usually 980 nm or 1480 nm) is propagated into the core of the fiber in order to excite its ions.
Excited ions, when ``hit'' by an input ``signal'' photon, have a certain probability (depending on the wavelength of the input photon) of releasing by stimulated emission a photon identical to the hitting one. The release of the energy of the stimulated photon brings the excited ion to its fundamental state.
Hence from one input ``signal'' photon we can obtain, by an avalanche process along the fiber core, an average of G photons at the fiber output, i.e., the signal photon has been amplified by a factor G, known as the Gain.
Since the probability of stimulated emission depends on the photon wavelength, so does the Gain.
The Gain clearly also depends on the total number of excited ions in the fiber, since the more the ions, the larger the average number of stimulated emissions per input photon.
In Optical Communication systems based on Wavelength Division Multiplexing,
N signal laser beams at N different wavelengths (each carrying modulated
user information) are coupled into the EDFA and propagate down the
fiber along with the pump. While the pump ``loses'' photons to excite
the ions as it propagates, the signals stimulate emission from the
excited ions and ``gain'' photons.

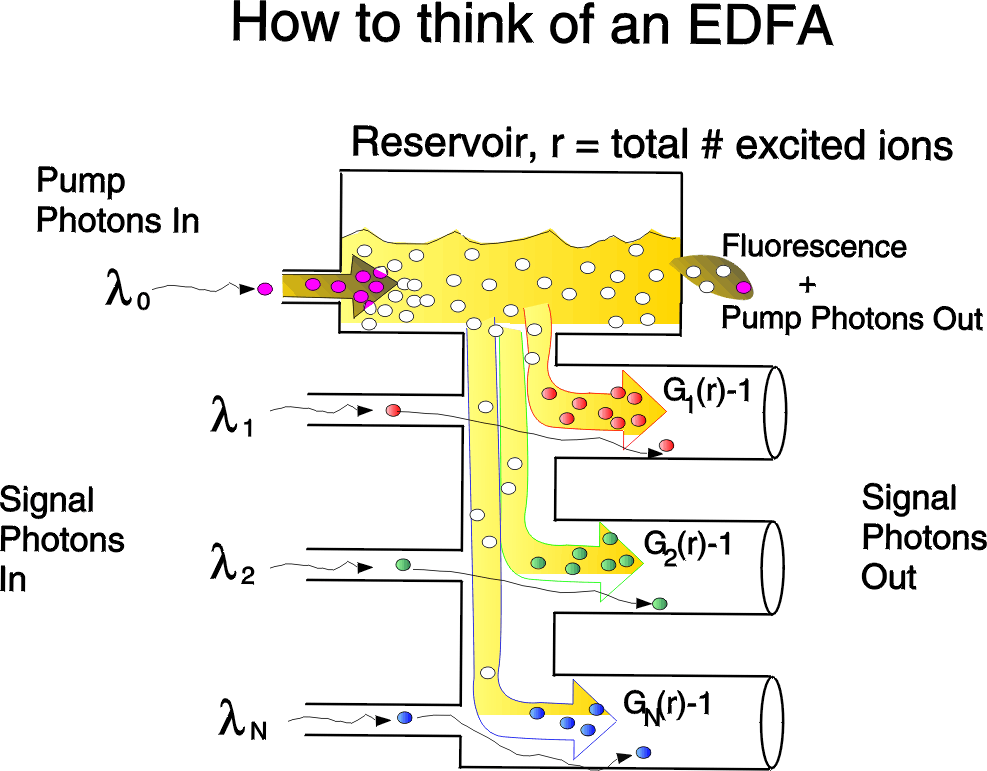
The figure shows a simple but correct way of thinking about the amplification process in the EDFA. This vision is derived from our paper:
[BRT_jlt_98] ``Doped fiber amplifier dynamics: a system perspective''.
The EDFA is a sort of ``hydraulic system'', composed of a tank containing a ``reservoir'' of charges (the white balls in the figure, physically corresponding to the excited ions in the fiber) ready to be converted into output photons by stimulated emission. The reservoir is limited to a maximum value, i.e., to the total number of ions in the doped fiber.
Consider now an input red photon (i.e., one at a specific wavelength, or color). As it enters the EDFA it draws from the reservoir on the average Gr-1 charges, which get colored the same color as the input photon and give at the output Gr signal photons (r stands for red, as the gain depends on wavelength).
The same is true for a green input photon, which draws an average of Gg-1 charges, or a blue input photon, drawing Gb-1 charges.
That is, all input signal photons draw charges from the same reservoir, which is therefore subject to oscillations when the signal photon fluxes (average number of input photons per second) abruptly vary in time due to the sudden addition of new channels or to the removal of existing channels. Such oscillations of the reservoir level occur like in any water basin.
The fact that all signals draw from the same reservoir is a consequence of what is known as the ``homogeneous broadening''. Since a lower reservoir level corresponds to a lower gain for all signals, the variations of the reservoir level correspond to variations of the gain and hence of the output signal photon fluxes, a phenomenon known as cross-gain modulation.
The tank in the figure is shown to have leakage of charges. This physically corresponds to fluorescence, i.e., the process of natural relaxation of ions from the excited state to the fundamental state, generating non-stimulated photons with wavelengths spread over a wide spectral range. The amplification of such photons along the amplifier generates the so-called amplified spontaneous emission noise (ASE). The figure, for simplicity of drawing, neglects the fact that the leakage flux actually enters the amplifier for amplification.
Finally, it is shown that the purple pump photons feed the reservoir. i.e., the purple photons enter the tank and lose their color as they get converted into excited ions. Some purple pump photons are also shown in the leakage flux, as not all pump photons are absorbed by the dopant ions.