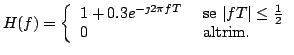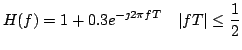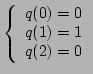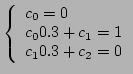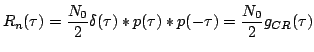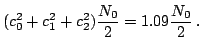Next: About this document ...
COMUNICAZIONI ELETTRICHE
Diploma Universitario
Ingegneria Elettronica - Ingegneria Informatica
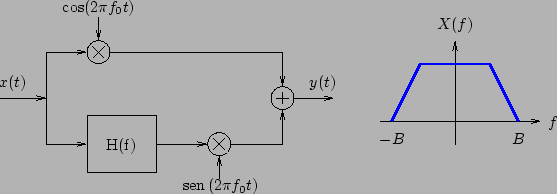
ESERCIZIO 1: Si consideri il sistema mostrato in figura. Il filtro ha risposta in frequenza
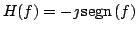 , dove la funzione
, dove la funzione
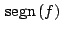 risulta essere definita come
Ponendo in ingresso al sistema il segnale
risulta essere definita come
Ponendo in ingresso al sistema il segnale 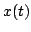 il cui spettro è mostrato in figura, si determini lo spettro del segnale
il cui spettro è mostrato in figura, si determini lo spettro del segnale 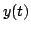 .
.
SOLUZIONE ESERCIZIO 1: Dallo schema a blocchi di figura possiamo ricavare l'espressione analitica del segnale 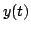 :
:
Passando nel dominio della frequenza, otteniamo
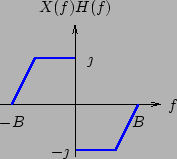
Poichè, all'uscita del filtro 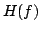 abbiamo un segnale con trasformata di Fourier come indicato in figura
siamo quindi in grado di disegnare le risposte in frequenza delle due parentesi quadrate con cui abbiamo scritto il segnale
abbiamo un segnale con trasformata di Fourier come indicato in figura
siamo quindi in grado di disegnare le risposte in frequenza delle due parentesi quadrate con cui abbiamo scritto il segnale 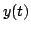 . Infatti dalla prima ricaviamo
mentre dalla seconda ricaviamo
Sommando infine i due termini otteniamo lo spettro di figura, dal quale si deduce che lo schema a blocchi presentato effettua una modulazione SSB-LB.
. Infatti dalla prima ricaviamo
mentre dalla seconda ricaviamo
Sommando infine i due termini otteniamo lo spettro di figura, dal quale si deduce che lo schema a blocchi presentato effettua una modulazione SSB-LB.
ESERCIZIO 2: Un segnale PAM ha espressione
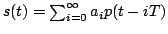 . I simboli
. I simboli 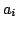 , equiprobabili ed indipendenti, appartengono all'alfabeto
, equiprobabili ed indipendenti, appartengono all'alfabeto 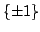 , mentre l'impulso
, mentre l'impulso 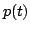 ha trasformata di Fourier
ha trasformata di Fourier
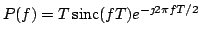 , con
, con
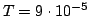 s.
s.
- Si determini la densità spettrale di potenza
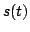 e se ne disegni il grafico.
e se ne disegni il grafico.
- Il segnale è trasmesso su un canale che introduce rumore additivo gaussiano bianco con densità spettrale di potenza
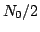 , con
, con
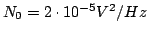 . In ricezione si utilizza lo schema mostrato in figura, in cui DEC è un decisore a soglia con soglia zero. Si determini la probabilità d'errore di tale sistema.
. In ricezione si utilizza lo schema mostrato in figura, in cui DEC è un decisore a soglia con soglia zero. Si determini la probabilità d'errore di tale sistema.
SOLUZIONE ESERCIZIO 2: Per poter ricavare l'espressione analitica della densità spettrale di potenza di 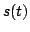 , occorre per prima cosa individuare la sequenza di autocorrelazione della sequenza di informazione
, occorre per prima cosa individuare la sequenza di autocorrelazione della sequenza di informazione 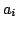 . In particolare essa risulta uguale a
. In particolare essa risulta uguale a
Calcoliamo quindi il valor medio e la varianza di tale sequenza: abbiamo che il valor medio risulta essere dato da
mentre la varianza risulta essere
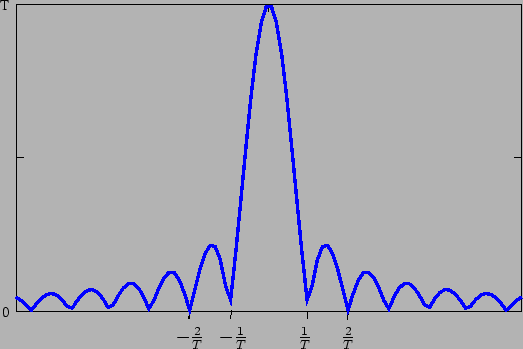
Dalla teoria sappiamo che un segnale modulato PAM ha uno spettro di potenza dato dalla espressione
Poichè i simboli di informazione sono a media nulla, nello spettro di potenza non compaiono delle righe, per cui otteniamo
il cui grafico è riportato in figura.
All'uscita del blocco integratore otteniamo una versione discretizzata del segnale ricevuto. Infatti si ha
dove
Possiamo quindi scrivere
Possiamo, a questo punto, fare alcune osservazioni. Il rumore gaussiano bianco additivo risulta essere filtrato dalla risposta all'impulso dell'integratore a finestra mobile. Calcoliamo perciò la sua potenza:
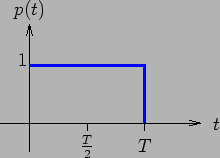
Occorre quindi avere nota l'espressione analitica dell'impulso formante 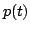 e poi effettuare l'operazione di integrazione. In figura è quindi riportato l'andamento, nel tempo, dell'impulso
e poi effettuare l'operazione di integrazione. In figura è quindi riportato l'andamento, nel tempo, dell'impulso 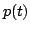 .
Possiamo quindi calcolare la potenza di rumore:
Possiamo inoltre osservare come l'impulso formante non introduca interferenza intersimbolica, in quanto a durata finita e pari all'intervallo di segnalazione
.
Possiamo quindi calcolare la potenza di rumore:
Possiamo inoltre osservare come l'impulso formante non introduca interferenza intersimbolica, in quanto a durata finita e pari all'intervallo di segnalazione 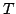 .
Calcoliamo infine la probabilità d'errore
.
Calcoliamo infine la probabilità d'errore 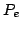 : abbiamo
: abbiamo
ESERCIZIO 3: Un segnale PAM ha espressione
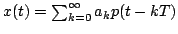 . I simboli
. I simboli  , equiprobabili ed indipendenti, appartengono all'alfabeto
, equiprobabili ed indipendenti, appartengono all'alfabeto 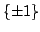 , mentre l'impulso
, mentre l'impulso 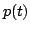 ha trasformata di Fourier
a radice di coseno rialzato, con roll-off uguale a
ha trasformata di Fourier
a radice di coseno rialzato, con roll-off uguale a 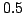 e con intervallo di segnalazione
e con intervallo di segnalazione
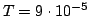 s. Si vuole trasmettere il segnale su un canale affetto da rumore Gaussiano bianco additivo, con densità spettrale di potenza
s. Si vuole trasmettere il segnale su un canale affetto da rumore Gaussiano bianco additivo, con densità spettrale di potenza 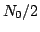 , con
, con
 .
.
- Ipotizzando infine che il canale di trasmissione abbia funzione di trasferimento pari a
al fine di ridurre il più possibile l'interferenza intersimbolica introdotta, dimensionare un equalizzatore a 3 prese.
- Calcolare la potenza del rumore termico all'uscita di tale filtro.
SOLUZIONE ESERCIZIO 3: La risposta in frequenza del canale risulta essere perció
da cui è possibile ricavare la risposta all'impulso del canale
Come stadio di ricezione, consideriamo un ricevitore a filtro adattato all'impulso di tipo a radice di coseno rialzato e campionatore a frequenza di simbolo.
L'impulso 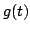 all'uscita del filtro di ricezione avrà spettro del tipo
e quindi l'impulso
all'uscita del filtro di ricezione avrà spettro del tipo
e quindi l'impulso 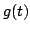 risulterà essere
dove con
risulterà essere
dove con 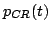 si è indicato l'impulso complessivo a coseno rialzato: supponiamo inoltre che
si è indicato l'impulso complessivo a coseno rialzato: supponiamo inoltre che
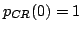 . All'uscita del campionatore a intervalli
. All'uscita del campionatore a intervalli 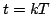 otteniamo l'impulso discreto
per cui il segnale su cui effettuare la decisione risulta essere
Dimensioniamo quindi un equalizzatore a 3 prese. L'impulso
otteniamo l'impulso discreto
per cui il segnale su cui effettuare la decisione risulta essere
Dimensioniamo quindi un equalizzatore a 3 prese. L'impulso 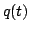 all'uscita dell'equalizzatore può essere espresso come
dove
all'uscita dell'equalizzatore può essere espresso come
dove
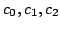 sono i coefficienti delle prese dell'equalizzatore. Abbiamo quindi
sono i coefficienti delle prese dell'equalizzatore. Abbiamo quindi
Imponendo le condizioni
dalla (1) si ottiene il sistema
la cui risoluzione porta ad avere
Calcoliamo infine la potenza del rumore termico in uscita dall'equalizzatore. Abbiamo che il rumore termico 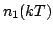 dopo l'equalizzatore può essere espresso in funzione del rumore
dopo l'equalizzatore può essere espresso in funzione del rumore 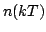 prima di tale equalizzatore
Poiché l'autocorrelazione del processo
prima di tale equalizzatore
Poiché l'autocorrelazione del processo 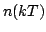 risulta essere il campionamento di quella del processo tempo continuo
risulta essere il campionamento di quella del processo tempo continuo 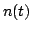 abbiamo
da cui è possibile calcolare la varianza
abbiamo
da cui è possibile calcolare la varianza
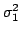 del processo
del processo 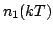 che, essendo a media nulla, coincide con il valore quadratico medio. Ricordando infine che i campioni
che, essendo a media nulla, coincide con il valore quadratico medio. Ricordando infine che i campioni 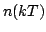 del processo di rumore a tempo continuo
del processo di rumore a tempo continuo 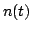 sono indipendenti (perchè?), abbiamo
sono indipendenti (perchè?), abbiamo



Next: About this document ...
Riccardo Pighi
2004-05-06


![]() :
:
![$\displaystyle Y(f) = \frac{1}{2} \left[X(f - f_0) + X(f + f_0) \right] + \frac{1}{2\jmath} \left[X(f - f_0)H(f - f_0) - X(f + f_0)H(f + f_0) \right]
$](img8.png)
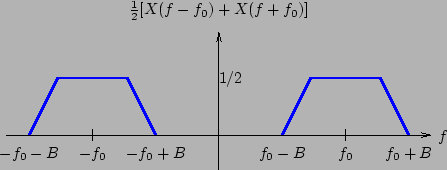
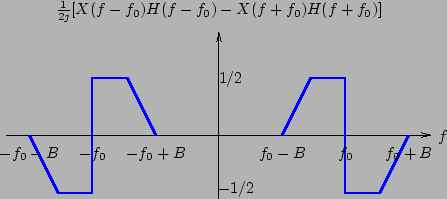
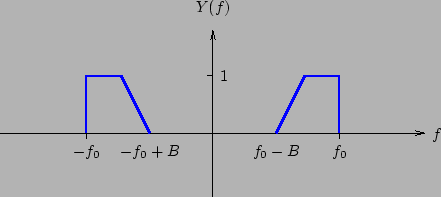
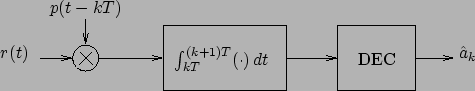
![]() , occorre per prima cosa individuare la sequenza di autocorrelazione della sequenza di informazione
, occorre per prima cosa individuare la sequenza di autocorrelazione della sequenza di informazione ![]() . In particolare essa risulta uguale a
. In particolare essa risulta uguale a
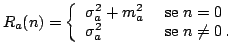

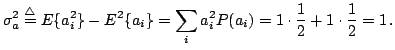
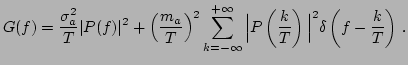
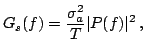
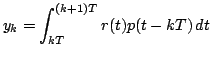
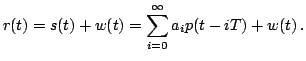
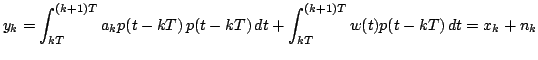
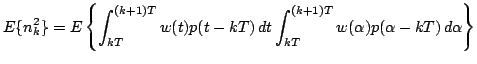

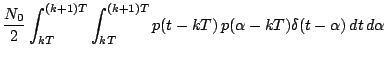
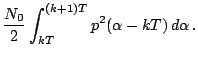
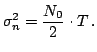
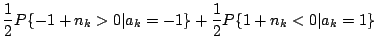
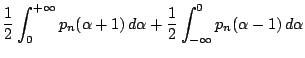
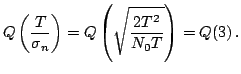
![]() . I simboli
. I simboli ![]() , equiprobabili ed indipendenti, appartengono all'alfabeto
, equiprobabili ed indipendenti, appartengono all'alfabeto ![]() , mentre l'impulso
, mentre l'impulso ![]() ha trasformata di Fourier
a radice di coseno rialzato, con roll-off uguale a
ha trasformata di Fourier
a radice di coseno rialzato, con roll-off uguale a ![]() e con intervallo di segnalazione
e con intervallo di segnalazione
![]() s. Si vuole trasmettere il segnale su un canale affetto da rumore Gaussiano bianco additivo, con densità spettrale di potenza
s. Si vuole trasmettere il segnale su un canale affetto da rumore Gaussiano bianco additivo, con densità spettrale di potenza ![]() , con
, con
![]() .
.