


Next: About this document ...
Up: equalizzatori
Previous: Introduzione
Se quindi campioniamo l'impulso equalizzato, otteniamo
cioè otteniamo la convoluzione discreta tra i campioni del filtro di equalizzazione ed i campioni dell'impulso 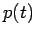 . Dalla conoscenza dei campioni
, determiniamo i campioni dell'equalizzatore. Teoricamente vorremmo ottenere infiniti zeri ed un valore massimo in coincidenza dell'istante di campionamento. Poiché però abbiamo a disposizione solo
. Dalla conoscenza dei campioni
, determiniamo i campioni dell'equalizzatore. Teoricamente vorremmo ottenere infiniti zeri ed un valore massimo in coincidenza dell'istante di campionamento. Poiché però abbiamo a disposizione solo 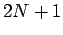 valori di
, riusciremo solo ad avere
zeri. Riusciremo quindi a non avere ISI solo per un certo numero di campioni intorno all'istante di campionamento.
valori di
, riusciremo solo ad avere
zeri. Riusciremo quindi a non avere ISI solo per un certo numero di campioni intorno all'istante di campionamento.
Per ottenere i pesi dell'equalizzatore, occorre risolvere il semplice sistema lineare ottenuto imponendo la condizione (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ):
):
Nell'esempio successivo si presenta il progetto di un equalizzatore numerico.
ESERCIZIO: Un segnale PAM ha espressione
. I simboli 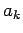 , equiprobabili ed indipendenti, appartengono all'alfabeto
, mentre l'impulso
, equiprobabili ed indipendenti, appartengono all'alfabeto
, mentre l'impulso 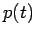 ha trasformata di Fourier
a radice di coseno rialzato, con roll-off uguale a
e con intervallo di segnalazione
s. Si vuole trasmettere il segnale su un canale affetto da rumore Gaussiano bianco additivo, con densità spettrale di potenza
.
ha trasformata di Fourier
a radice di coseno rialzato, con roll-off uguale a
e con intervallo di segnalazione
s. Si vuole trasmettere il segnale su un canale affetto da rumore Gaussiano bianco additivo, con densità spettrale di potenza
.
- Ipotizzando infine che il canale di trasmissione abbia funzione di trasferimento pari a
al fine di ridurre il più possibile l'interferenza intersimbolica introdotta, dimensionare un equalizzatore a 3 prese.
|
|---|
SOLUZIONE: La risposta in frequenza del canale risulta essere perció
da cui è possibile ricavare la risposta all'impulso del canale
Come stadio di ricezione, consideriamo un ricevitore a filtro adattato all'impulso di tipo a radice di coseno rialzato e campionatore a frequenza di simbolo.
L'impulso
all'uscita del filtro di ricezione avrà spettro del tipo
e quindi l'impulso
risulterà essere
dove con
si è indicato l'impulso complessivo a coseno rialzato: supponiamo inoltre che
. All'uscita del campionatore a intervalli
otteniamo l'impulso discreto
per cui il segnale su cui effettuare la decisione risulta essere
Dimensioniamo quindi un equalizzatore a 3 prese. L'impulso
all'uscita dell'equalizzatore può essere espresso come
dove
sono i coefficienti delle prese dell'equalizzatore. Abbiamo quindi
Imponendo le condizioni
si ottiene
Infine, sostituendo nella (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) i campioni dell'impulso
, si ottiene il sistema
) i campioni dell'impulso
, si ottiene il sistema
la cui risoluzione porta ad avere



Next: About this document ...
Up: equalizzatori
Previous: Introduzione
Riccardo Pighi
2005-06-21
![]() ):
):